一、2017年美国大学生数学建模竞赛

1.项目名称：收费站后的车流合并问题

项目成员：吴骄阳 高志灵 赵壮

指导教师：侯强

项目简介：对于一条具有L条车道的高速公路的收费广场，我们对其扇入区的形状，尺寸，合并模式进行了设计，使其在事故预防，吞吐量以及成本方面达到最优。对于合并模式，我们选择（2-into-1）的合并点，然后建立收费广场排队论模型，得出车辆通过收费广场总的延误时间

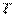；针对扇入区域的形状，在优化的边界形状方案基础上，我们提出缓和曲线模型，并用此模型对扇入区的边界进一

步优化设计，提高了车辆通过扇入区的安全性能，降低了发生事故的概率；之后又考虑扇入区沿高速公路方向上的安全距离 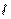    ，建立扇入区的面积模型，进而得出扇入区土地与道路建设成本 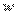    ，以此作为尺寸设计依据。最后通过仿真模拟对我们的设计作出最终修改与评价。

2.项目名称：收费广场设计

项目成员：李尧董兴琨吴健健

指导教师：陆平

项目简介：我们对收费广场的形状，尺寸，尤其是过卡后的并流模式进行了最优设计，以吞吐量作为衡量设计效果的最主要标准。因收费广场由三部分组成，我们分别计算出每一部分延迟时间进而计算出吞吐量。根据流体力学建立车辆进入收费广场的延误时间模型和建立了排队论模型计算车流通过收费站的延误时间及基于马尔可夫系统，我们建立过卡后并流模型，并通过数值模拟，比较了在较小车流量、较大车流量情况下边缘合并和中间提前合并的延误时间及其安全性，得出边缘合并方式更优。

二、全国大学生数学建模大赛

项目名称：小区开放对道路通行的影响

项目成员：李尧董兴坤彭虹琅

指导老师:雷英杰

项目简介：开放小区将周边道路网，对缓解城市交通压力有最大意义。我们将建立合适的数学模型研究小区开放对周边道路影响来确定小区开放对周边道路影响进行定量分析。采用层次分析法从道路交通服务水平指标、出入口及主要交叉口通行、停车设施适应性指标、公共交通适应性指标这四个方面进行讨论分析，并将美国联邦公路局路阻函数（BPR函数）修正改良，利用改良后的BPR函数计算行程时间可靠度，我们用准确性比较高的Weibull分布求行程时间可靠度，经过代换得出路径可靠度与行程时间可靠度的函数关系式，路径可靠度构成OD对可靠度，多个OD对构成了路网，路网可靠度是路网正常使用条件下，某特定时段内能满足畅通可达的概率。路网可靠度指标作为一个概率性指标很好地体现了路网系统的稳定性，以及道路交通系统的功能和效率。

三.第五届全国大学生工程训练综合能力竞赛

参赛学生：陈兴旺李尧李建国

指导老师：李晓宏孔为民

作品简介：利用下落的重锤将重力势能转换为动能驱动自身行走并且自动避开障碍物。为了方便设计这里根据小车所要完成的功能将小车划分为四个部分进行模块化设计：原动机构、传动机构、转向机构、行走机构、微调机构。采用绳轮作为原动机构。绳轮机构简单，传动效率高，且在针对不同场地导致的所需动力不同的情况可通过调节绕绳位置来改变转矩，使动力改变，增强适应性本方案采用绳轮作为驱动力转换机构。用曲柄连杆+摇杆作为转向机构，单轮驱动，加载螺旋测微器作为微调机构实现小车在光滑平整的地面做“S”轨迹运动。